无权二分图的匹配

发表于 | 分类于 | 阅读次数 |
字数统计 2,200

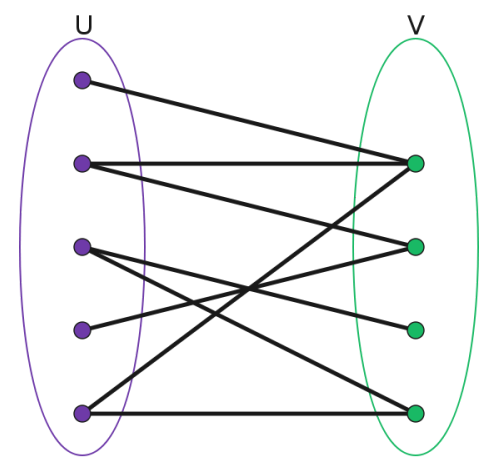
image

二分图:
又称作二部图，是图论中的一种特殊模型。 设$G=(V,E)$是一个无向图，如果顶点$V$可分割为两个互不相交的子集$(A,B)$，并且图中的每条边$（i，j）$所关联的两个顶点$i$和$j$分别属于这两个不同的顶点集$(i \in A,j \in B)$，则称图$G$为一个二分图。

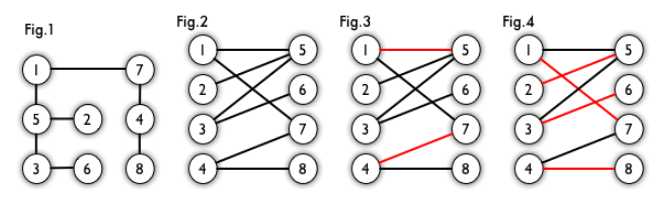
二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

image

颜色法判断是否为二分图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e6 + 10, M = 2 * N;

int h[N], e[M], ne[M], idx;
int color[N];
int n, m;

// 头插法
void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}

bool dfs(int u, int c)
{
    color[u] = c;
    
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!color[j])
        {
            if (!dfs(j, 3 - c)) return false; // 给下一个点相反的颜色
        }
        else if (color[j] == c) return false; // 相邻点不能为同一颜色
    }
    
    return true;
}

int main()
{
    memset(h, -1, sizeof h); // init
    
    cin >> n >> m;
    for (int i = 0; i < m; i ++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); // 头插法连接图
    }
    
    bool flag = true; // 是否为二分图
    for (int i = 1; i <= n; i ++) // 数据从1开始
        if (!color[i])
        {
            if (!dfs(i, 1))
            {
                flag = false;
                break;
            }
        }
    
    if (flag) puts("Yes");
    else puts("No");
    
    return 0;
}

匹配:
在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配:
一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：
如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。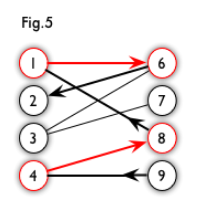
image
交替路：
从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边… 形成的路径叫交替路。
9 -> 4 -> 8 -> 1 -> 6

增广路：
从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。
9 -> 4 -> 8 -> 1 -> 6 -> 2

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。

匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。例如，由图 7，可以得到如图 8 的一棵 BFS 树：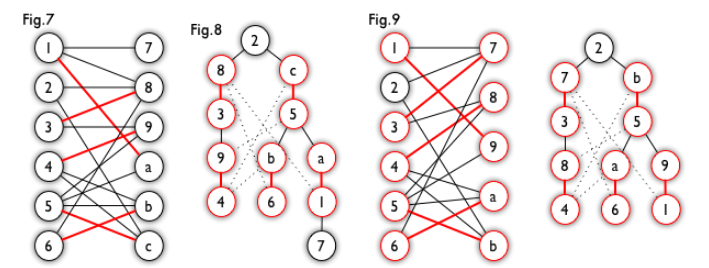
image

这棵树存在一个叶子节点为非匹配点（7 号），但是匈牙利树要求所有叶子节点均为匹配点，因此这不是一棵匈牙利树。如果原图中根本不含 7 号节点，那么从 2 号节点出发就会得到一棵匈牙利树。这种情况如图 9 所示（顺便说一句，图 8 中根节点 2 到非匹配叶子节点 7 显然是一条增广路，沿这条增广路扩充后将得到一个完美匹配）。

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
M=[]


class DFS_hungary():
    def __init__(self, nx, ny, edge, cx, cy, visited):
        self.nx, self.ny=nx, ny
        self.edge = edge
        self.cx = cx
        self.cy = cy
        self.visited = visited

    def max_match(self):
        res=0
        for i in self.nx:
            if self.cx[i]==-1:
                for key in self.ny: # 将visited置0表示未访问过
                    self.visited[key]=0
                res+=self.path(i)
        return res

    def path(self, u):
        for v in self.ny:
            if self.edge[u][v] and (not self.visited[v]):
                self.visited[v]=1
                if self.cy[v]==-1:
                    self.cx[u] = v
                    self.cy[v] = u
                    M.append((u,v))
                    return 1
                else:
                    M.remove((self.cy[v], v))
                    if self.path(self.cy[v]):
                        self.cx[u] = v
                        self.cy[v] = u
                        M.append((u, v))
                        return 1
        return 0


if __name__ == '__main__':
    nx, ny = ['A', 'B', 'C', 'D'], ['E', 'F', 'G', 'H']
    edge = {'A':{'E': 1, 'F': 0, 'G': 1, 'H':0}, 'B':{'E': 0, 'F': 1, 'G': 0, 'H':1}, 'C':{'E': 1, 'F': 0, 'G': 0, 'H':1}, 'D':{'E': 0, 'F': 0, 'G': 1, 'H':0}} # 1 表示可以匹配， 0 表示不能匹配
    cx, cy = {'A':-1,'B':-1,'C':-1,'D':-1}, {'E':-1,'F':-1,'G':-1,'H':-1}
    visited = {'E': 0, 'F': 0, 'G': 0,'H':0}

    print(DFS_hungary(nx, ny, edge, cx, cy, visited).max_match())

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <iostream>
#include <cstring>

using namespace std;

const int N = 510, M = 100010;

int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];
int n1, n2, m;

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}

bool find(int u)
{
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true;
            if (match[j] == 0 || find(match[j])) // 当前匹配到的另一边未匹配，或者已经匹配的人有其他匹配选择
            {
                match[j] = u; //更新匹配给u
                return true;
            }
        }
    }
    
    return false;
}

int main()
{
    memset(h, -1, sizeof h);

    cin >> n1 >> n2 >> m;
    while(m --)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    
    int res = 0;
    // 选择一边进行匹配
    for (int i = 1; i <= n1; i ++)
    {
        memset(st, false, sizeof st);
        if (find(i)) res ++;
    }
    
    printf("%d\n", res);
    
    return 0;
}

匈牙利算法的要点如下:

  • 从左边第 1 个顶点开始，挑选未匹配点进行搜索，寻找增广路。

    • 如果经过一个未匹配点，说明寻找成功。更新路径信息，匹配边数 +1，停止搜索。
    • 如果一直没有找到增广路，则不再从这个点开始搜索。事实上，此时搜索后会形成一棵匈牙利树。我们可以永久性地把它从图中删去，而不影响结果。

  • 由于找到增广路之后需要沿着路径更新匹配，所以我们需要一个结构来记录路径上的点。DFS 版本通过函数调用隐式地使用一个栈，而 BFS 版本使用 prev 数组。

性能比较:

两个版本的时间复杂度均为$O(V⋅E)$。DFS 的优点是思路清晰、代码量少，但是性能不如 BFS。我测试了两种算法的性能。对于稀疏图，BFS 版本明显快于 DFS 版本；而对于稠密图两者则不相上下。在完全随机数据 9000 个顶点 4,0000 条边时前者领先后者大约 97.6%，9000 个顶点 100,0000 条边时前者领先后者 8.6%, 而达到 500,0000 条边时 BFS 仅领先 0.85%。

补充定义和定理：

最大匹配数：最大匹配的匹配边的数目

最小点覆盖数：选取最少的点，使任意一条边至少有一个端点被选择

最大独立数：选取最多的点，使任意所选两点均不相连

最小路径覆盖数：对于一个 DAG（有向无环图），选取最少条路径，使得每个顶点属于且仅属于一条路径。路径长可以为 0（即单个点）。

定理1：最大匹配数 = 最小点覆盖数（这是 Konig 定理）

定理2：最大匹配数 = 最大独立数

定理3：最小路径覆盖数 = 顶点数 - 最大匹配数

兴趣使然